Bézier Curve Tool

About the tool

I was playing around with some SVG paths and getting frustrated with defining some curves - I couldn't make the link between setting the control points and how the curve… curved.

I tried searching for some tutorials or other descriptions of how cubic Bézier curves worked, but all I got was a lot of dense mathematics articles. Eventually I was able to get what I wanted through trial and error, but decided I needed a visual tool to help in the future.

So here it is. A zero-maths tool for generating curvy paths. Set your points and anchors, and a path specification will output on the right.

It works on touch screens, too.

Cubic Bézier curves

an example Bézier curve between two points

B(t ) = (1 - t )3BP0,P1,P2(t )+t BP1,P2,P3(t ) , 0 ≤ t ≤ 1

Got that? Yeah, me neither. (If you do, then kudos - but I haven't dealt with Maths like this since graduating from university in 2000).

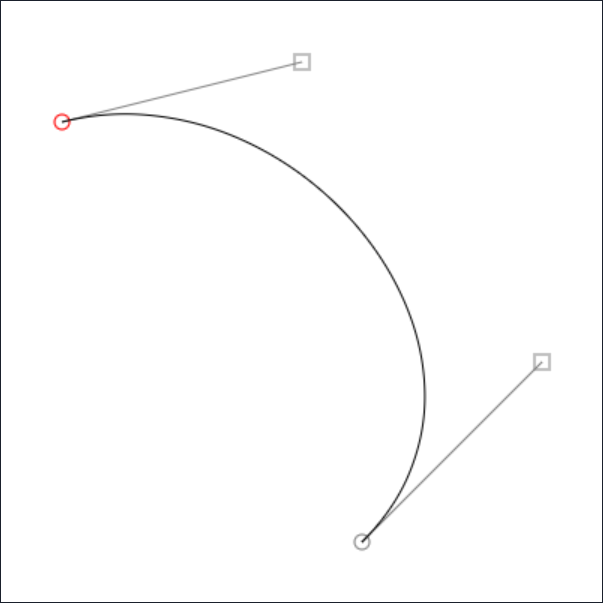
The basic idea behind a cubic Bézier curve is that you have a start and end point, and then you have two control points (or anchors). With these four points you can define a curve.

Both SVG and the Canvas API have functions to handle the maths for you, so all you have to know is where you want the four points to be. But how do you know where the points should be for the curve you want?

If you want to know more about Bézier curves, there's Wikipedia or this in-depth primer.

Built with